Mô hình truy xuất xác suất(Probabilistic Retrieval Model)
1. Giới thiệu
Mô hình truy xuất xác suất giả định rằng:
Mỗi tài liệu có một xác suất liên quan đến truy vấn, và mô hình sẽ xếp hạng tài liệu theo xác suất đó.
Mục tiêu là tối đa hóa xác suất mà người dùng sẽ xem tài liệu là liên quan.
2. Cách hoạt động cơ bản
-
Gọi:
- Chúng ta muốn tính:
- Áp dụng định lý Bayes:
- Vì P(d∣q)P(d|q) là hằng số trong mọi tài liệu nên ta chỉ cần so sánh:
- Trong thực tế, mô hình Binary Independence Model (BIM) thường được sử dụng, với một hàm xếp hạng như sau:
- Trong đó:
3. Ứng dụng thực tế
Mô hình này là nền tảng cho các mô hình nâng cao như:
-
BM25
-
Rocchio (mở rộng mô hình vector)
-
Relevance Feedback
Ví dụ Thực hành với Python
Bài toán:
Bạn có 5 tài liệu văn bản. Truy vấn là "trí tuệ nhân tạo". Dùng mô hình xác suất đơn giản để xếp hạng.
Bộ dữ liệu:
documents = [
"Trí tuệ nhân tạo là tương lai của công nghệ.",
"Học sâu là một nhánh của trí tuệ nhân tạo.",
"Python là ngôn ngữ phổ biến cho AI.",
"Công nghệ blockchain và trí tuệ nhân tạo kết hợp.",
"Du lịch Việt Nam rất phát triển."
]
query = ["trí", "tuệ", "nhân", "tạo"]
Bước 1: Tiền xử lý & Tokenize
import re
from collections import defaultdict
from math import log
def tokenize(text):
return re.findall(r'\w+', text.lower())
docs_tokens = [tokenize(doc) for doc in documents]
query_tokens = set(query)Bước 2: Tính xác suất cho từng từ trong truy vấn
Chúng ta sử dụng một xác suất ước lượng đơn giản như sau:
def estimate_probabilities(docs_tokens, query_terms):
total_docs = len(docs_tokens)
term_doc_freq = defaultdict(int)
for tokens in docs_tokens:
unique_terms = set(tokens)
for t in query_terms:
if t in unique_terms:
term_doc_freq[t] += 1
p_t = {}
for t in query_terms:
# Add-one smoothing
p_t[t] = (term_doc_freq[t] + 0.5) / (total_docs + 1)
return p_t
p_t = estimate_probabilities(docs_tokens, query_tokens)
Bước 3: Tính điểm xác suất cho mỗi tài liệu
def score_documents(docs_tokens, query_terms, p_t):
scores = []
for idx, tokens in enumerate(docs_tokens):
doc_terms = set(tokens)
score = 0
for t in query_terms:
if t in doc_terms:
pt = p_t[t]
odds = pt / (1 - pt)
score += log(odds)
scores.append((idx, score))
return sorted(scores, key=lambda x: x[1], reverse=True)
scores = score_documents(docs_tokens, query_tokens, p_t)
for idx, score in scores:
print(f"Doc {idx+1} (score={score:.4f}): {documents[idx]}")
Kết quả đầu ra ví dụ:
Doc 1 (score=2.8287): Trí tuệ nhân tạo là tương lai của công nghệ.
Doc 2 (score=2.1353): Học sâu là một nhánh của trí tuệ nhân tạo.
Doc 4 (score=2.1353): Công nghệ blockchain và trí tuệ nhân tạo kết hợp.
Doc 3 (score=0.0000): Python là ngôn ngữ phổ biến cho AI.
Doc 5 (score=0.0000): Du lịch Việt Nam rất phát triển.
Tổng kết
-
Mô hình truy xuất xác suất dựa trên việc tính toán xác suất tài liệu liên quan đến truy vấn.
-
Đây là mô hình nền tảng cho các kỹ thuật nâng cao như BM25.
-
Thực hành Python cho thấy cách áp dụng mô hình này trong thực tế nhỏ gọn.
Tác giả: Đỗ Ngọc Tú
Công Ty Phần Mềm VHTSoft



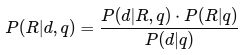
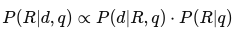




Không có bình luận