Tóm tắt dữ liệu định lượng
Dữ liệu định lượng (Quantitative data) là loại dữ liệu thể hiện bằng số lượng hoặc con số, phản ánh mức độ, số lần, trọng lượng, chiều dài, thời gian, v.v. Đây là dữ liệu có thể đo lường được bằng các đơn vị cụ thể và có thể thực hiện các phép tính toán học (cộng, trừ, trung bình, độ lệch chuẩn, v.v.).
Phân loại dữ liệu định lượng
Dữ liệu định lượng được chia thành hai loại chính:
-
Dữ liệu rời rạc (Discrete data)
-
Là dữ liệu chỉ nhận các giá trị nguyên, thường là kết quả của việc đếm.
-
Ví dụ: số sinh viên trong lớp, số xe bán ra mỗi tháng, số cuộc gọi trong ngày.
-
-
Dữ liệu liên tục (Continuous data)
-
Là dữ liệu có thể nhận bất kỳ giá trị nào trong một khoảng, thường là kết quả của việc đo lường.
-
Ví dụ: chiều cao, cân nặng, nhiệt độ, thời gian, tốc độ...
-
Đặc điểm của dữ liệu định lượng
-
Có thể sắp xếp theo thứ tự và tính toán được.
-
Có thể biểu diễn bằng các biểu đồ như: biểu đồ cột, biểu đồ histogram, biểu đồ đường, biểu đồ tròn (nếu đã phân nhóm).
Phân phối tần số dữ liệu định lượng
Như đã định nghĩa trong Mục 2.1, phân phối tần số là một bảng tóm tắt dữ liệu cho thấy số lượng (tần số) của các mục trong mỗi lớp không chồng lấp nhau. Định nghĩa này áp dụng cho cả dữ liệu định tính lẫn định lượng. Tuy nhiên, với dữ liệu định lượng, việc xác định các lớp không chồng lấp thường phức tạp hơn.
Hãy xét đến dữ liệu định lượng trong Bảng 2.4. Dữ liệu này cho biết số ngày cần thiết để hoàn thành các cuộc kiểm toán cuối năm đối với một mẫu gồm 20 khách hàng của công ty kế toán nhỏ Sanderson và Clifford. Dữ liệu đã được làm tròn đến ngày gần nhất. Có ba bước cần thiết để xác định các lớp trong phân phối tần số đối với dữ liệu định lượng như sau:
-
Xác định số lượng lớp không chồng lấp.
-
Xác định độ rộng của mỗi lớp.
-
Xác định giới hạn của mỗi lớp.
1. Số lượng lớp
Các lớp được hình thành bằng cách xác định các khoảng giá trị sẽ được sử dụng để nhóm dữ liệu. Theo nguyên tắc chung, chúng tôi khuyến nghị sử dụng từ 5 đến 20 lớp.
Với mẫu dữ liệu nhỏ, chỉ cần khoảng 5 hoặc 6 lớp là đủ để tóm tắt dữ liệu. Đối với các mẫu lớn hơn, thường cần nhiều lớp hơn.
Mục tiêu là sử dụng đủ số lớp để thể hiện được mô hình biến thiên trong dữ liệu, nhưng không nên quá nhiều đến mức khiến một số lớp chỉ chứa rất ít giá trị.
Vì mẫu dữ liệu trong Bảng 2.4 tương đối nhỏ (n = 20), nên chúng tôi chọn xây dựng bảng phân phối tần số gồm năm lớp.
| STT | Thời gian (ngày) | STT | Thời gian (ngày) |
|---|---|---|---|
| 1 | 12 | 11 | 33 |
| 2 | 22 | 12 | 15 |
| 3 | 14 | 13 | 28 |
| 4 | 23 | 14 | 18 |
| 5 | 19 | 15 | 14 |
| 6 | 22 | 16 | 17 |
| 7 | 18 | 17 | 18 |
| 8 | 21 | 18 | 20 |
| 9 | 15 | 19 | 16 |
| 10 | 15 | 20 | 27 |
| 21 | 13 |
12, 22, 14, 23, 19, 22, 18, 21, 15, 33, 15, 28, 18, 14, 17, 18, 20, 16, 27, 13
có 20 giá trị, mỗi giá trị đại diện cho thời gian kiểm toán (tính bằng ngày) của một khách hàng.
Khi bạn có dữ liệu định lượng như thời gian (ngày, giờ, số tiền, số sản phẩm...), để dễ phân tích, người ta chia dữ liệu thành các khoảng giá trị, mỗi khoảng gọi là một lớp.
Ví dụ:
Nếu thời gian dao động từ 12 đến 33 ngày, bạn có thể chia như sau:
-
Lớp 1: 12–16
-
Lớp 2: 17–21
-
Lớp 3: 22–26
-
Lớp 4: 27–31
-
Lớp 5: 32–36
➡ Mỗi lớp là một khoảng không chồng lấp, dùng để đếm số lần xuất hiện các giá trị thuộc khoảng đó.
Tại sao chọn 5 lớp?
-
Nguyên tắc chung:
Trong thống kê mô tả, người ta thường chọn từ 5 đến 20 lớp, tùy thuộc vào:-
Kích thước mẫu
-
Mức độ chi tiết bạn muốn phân tích
-
-
Trường hợp bạn đang làm:
-
Bạn có 20 quan sát (n = 20)
-
Mẫu này không lớn, nên 5 lớp là đủ để thấy xu hướng mà không quá chi tiết
-
Nếu chia quá nhiều lớp (ví dụ 10 lớp), có thể mỗi lớp chỉ chứa 1–2 giá trị, làm cho phân tích không có ý nghĩa
-
Vì vậy, chọn 5 lớp giúp:
-
Đơn giản hóa dữ liệu
-
Dễ đọc, dễ vẽ biểu đồ
-
Thể hiện xu hướng rõ ràng
2. Độ rộng của các lớp
Bước thứ hai là chọn độ rộng cho các lớp. Theo một nguyên tắc chung, chúng tôi khuyến nghị nên dùng cùng một độ rộng cho tất cả các lớp. Điều này giúp giảm khả năng diễn giải sai lệch. Việc lựa chọn số lượng lớp và độ rộng lớp không phải là hai quyết định độc lập. Nếu số lượng lớp tăng lên thì độ rộng lớp sẽ nhỏ lại, và ngược lại.
Để xác định độ rộng lớp xấp xỉ, ta cần xác định giá trị lớn nhất và nhỏ nhất trong tập dữ liệu. Sau đó, có thể dùng biểu thức sau để tính độ rộng lớp xấp xỉ:
Độ rộng lớp xấp xỉ = (Giá trị lớn nhất – Giá trị nhỏ nhất) / Số lượng lớp
Độ rộng lớp xấp xỉ thu được có thể được làm tròn lên thành một giá trị dễ sử dụng hơn.
Ví dụ: nếu độ rộng lớp xấp xỉ là 9.28, ta có thể làm tròn lên thành 10.
Ví dụ cụ thể – Dữ liệu thời gian kiểm toán cuối năm
-
Giá trị lớn nhất: 33
-
Giá trị nhỏ nhất: 12
-
Số lớp: 5
Áp dụng công thức:
(33 – 12) / 5 = 4.2
Chúng tôi quyết định làm tròn lên và sử dụng độ rộng lớp là 5 ngày.
3. Giới hạn lớp (Class limits)
Giới hạn lớp cần được chọn sao cho mỗi giá trị dữ liệu chỉ thuộc vào duy nhất một lớp.
-
Giới hạn dưới của lớp xác định giá trị dữ liệu nhỏ nhất có thể nằm trong lớp đó.
-
Giới hạn trên của lớp xác định giá trị dữ liệu lớn nhất có thể nằm trong lớp đó.
Khi xây dựng bảng phân phối tần số cho dữ liệu định tính, chúng ta không cần xác định giới hạn lớp, vì mỗi mục dữ liệu đã tự nhiên thuộc về một lớp (hay một danh mục riêng biệt).
Tuy nhiên, với dữ liệu định lượng, việc xác định giới hạn lớp là cần thiết để biết giá trị dữ liệu nằm ở đâu.
Ví dụ: Dữ liệu thời gian kiểm toán
-
Chúng tôi chọn 10 ngày làm giới hạn dưới và 14 ngày làm giới hạn trên cho lớp đầu tiên.
→ Lớp này được ký hiệu là 10–14 trong Bảng 2.5.
→ Giá trị nhỏ nhất là 12, nằm trong lớp 10–14. -
Tiếp theo, lớp thứ hai có giới hạn là 15–19, rồi tiếp tục với:
-
20–24
-
25–29
-
30–34
-
→ Tổng cộng có năm lớp.
→ Giá trị lớn nhất là 33, nằm trong lớp 30–34.
Khoảng cách giữa hai giới hạn dưới liên tiếp chính là độ rộng lớp.
→ Ví dụ: 15 – 10 = 5
Bảng phân phối tần số
Bây giờ ta có thể tạo bảng phân phối tần số bằng cách đếm số lượng dữ liệu thuộc vào từng lớp.
Ví dụ:
-
Lớp 10–14 có 4 giá trị (12, 14, 14 và 13) → tần số là 4
-
Lớp 15–19 có 8 giá trị
-
Lớp 20–24 có 5 giá trị
-
Lớp 25–29 có 2 giá trị
-
Lớp 30–34 có 1 giá trị
| Thời gian kiểm toán (ngày) | Tần số |
|---|---|
| 10–14 | 4 |
| 15–19 | 8 |
| 20–24 | 5 |
| 25–29 | 2 |
| 30–34 | 1 |
| Tổng cộng | 20 |
Một số nhận xét từ bảng phân phối tần số
-
Thời gian kiểm toán xuất hiện nhiều nhất nằm trong lớp 15–19 ngày. Có 8/20 lần kiểm toán nằm trong lớp này.
-
Chỉ có một lần kiểm toán kéo dài từ 30 ngày trở lên.
Người đọc có thể rút ra các nhận xét khác tùy theo mục đích và mối quan tâm của họ.
Giá trị thực tiễn của bảng phân phối tần số là giúp chúng ta hiểu dữ liệu dễ dàng hơn so với khi nhìn vào danh sách dữ liệu chưa được tổ chức.
Lớp mở (Open-ended class)
Lớp mở là lớp chỉ có giới hạn dưới hoặc giới hạn trên.
Ví dụ: nếu có hai giá trị kiểm toán là 58 và 65 ngày, thay vì tạo thêm các lớp:
-
35–39
-
40–44
-
45–49
v.v...
→ ta có thể đơn giản hóa bằng cách tạo một lớp mở: “35 ngày trở lên”, với tần số là 2.
Thông thường, lớp mở được dùng ở cuối bảng phân phối.
Trung điểm lớp (Class midpoint)
Trong một số trường hợp, chúng ta muốn biết trung điểm của các lớp trong bảng phân phối tần số của dữ liệu định lượng.
Trung điểm lớp là giá trị nằm giữa giới hạn dưới và giới hạn trên của một lớp.
Ví dụ với dữ liệu thời gian kiểm toán:
-
Năm trung điểm lớp tương ứng là: 12, 17, 22, 27 và 32.
Phân phối tần số tương đối và tần số phần trăm
Chúng ta định nghĩa tần số tương đối và tần số phần trăm cho dữ liệu định lượng giống như với dữ liệu định tính.
-
Tần số tương đối là tỷ lệ giữa số quan sát thuộc về một lớp so với tổng số quan sát.
Với nn là tổng số quan sát: -
Tần số phần trăm là tần số tương đối nhân với 100.
Dựa vào tần số lớp trong Bảng 2.5 và tổng số quan sát n=20n = 20, Bảng 2.6 thể hiện tần số tương đối và tần số phần trăm cho dữ liệu thời gian kiểm toán.
Ví dụ:
-
Có 0.40, hay 40% các cuộc kiểm toán kéo dài từ 15 đến 19 ngày.
-
Chỉ có 0.05, hay 5% các cuộc kiểm toán kéo dài từ 30 ngày trở lên.
Những phân tích và nhận định sâu hơn có thể được rút ra từ Bảng 2.6.
BẢNG 2.6 – Phân phối tần số tương đối và phần trăm cho dữ liệu thời gian kiểm toán
| Thời gian kiểm toán (ngày) | Tần số tương đối | Tần số phần trăm |
|---|---|---|
| 10–14 | 0.20 | 20% |
| 15–19 | 0.40 | 40% |
| 20–24 | 0.25 | 25% |
| 25–29 | 0.10 | 10% |
| 30–34 | 0.05 | 5% |
| Tổng cộng | 1.00 | 100% |
Biểu đồ chấm (Dot plot)
Một trong những cách đơn giản nhất để tóm tắt dữ liệu bằng đồ họa là biểu đồ chấm.
Trục ngang thể hiện khoảng giá trị của các quan sát.
Mỗi giá trị dữ liệu được biểu diễn bằng một dấu chấm đặt phía trên trục ngang.
Hình 2.3 là biểu đồ chấm được tạo bằng phần mềm MINITAB cho dữ liệu thời gian kiểm toán trong Bảng 2.4.
Ba dấu chấm nằm phía trên số 18 trên trục ngang cho thấy có ba lần kiểm toán kéo dài 18 ngày.
Biểu đồ chấm giúp thể hiện chi tiết dữ liệu và rất hữu ích khi so sánh phân phối dữ liệu giữa hai hoặc nhiều mẫu.
Biểu đồ Tần số (Histogram)
Định nghĩa
Biểu đồ tần số là dạng biểu đồ hiển thị dữ liệu định lượng đã được tổng hợp trong bảng phân phối tần số, tần số tương đối hoặc tần số phần trăm. Trong đó:
-
Trục hoành (ngang): Thể hiện biến số cần phân tích (ví dụ: thời gian, giá trị).
-
Trục tung (dọc): Thể hiện tần số, tần số tương đối hoặc tần số phần trăm của từng lớp dữ liệu.
Mỗi lớp dữ liệu được biểu diễn bằng một hình chữ nhật có:
-
Đáy: Xác định bởi giới hạn lớp trên trục hoành.
-
Chiều cao: Tương ứng với tần số/tần số phần trăm của lớp đó.
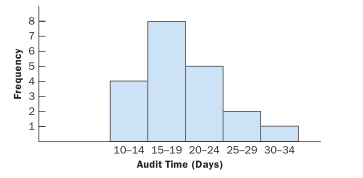
Ví dụ minh họa
Hình 2.5 dưới đây là biểu đồ tần số cho dữ liệu thời gian kiểm toán (đơn vị: ngày). Lớp có tần số cao nhất (15–19 ngày) được biểu diễn bằng hình chữ nhật cao nhất với tần số là 8. Nếu thay trục tung bằng tần số tương đối hoặc phần trăm, hình dạng biểu đồ vẫn giữ nguyên, chỉ khác ở giá trị trục dọc.

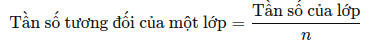

Không có bình luận